Старинные системы записи чисел

Тема урока:

Урок подготовила: Гаспарян Джульетта Эдуардовна

Система счисления первобытных людей

В каменном веке, когда люди собирали плоды, ловили рыбу и охотились на животных, потребность в счёте возникла так же естественно, как и потребность в добывании огня. Об этом свидетельствуют находки археологов на стоянках первобытного человека. Например, в 1937 г. в Вестонице (Моравия) на месте одной из таких стоянок обнаружена волчья кость с 55 глубокими зарубками. Позже в других местах учёные находили столь же древние каменные предметы с точками и чёрточками, сгруппированными по три или по пять. Такая система записи чисел называется единичной, так как любое число в ней образуется путём повторения одного знака, символизирующего единицу. Группировки и вспомогательные значки используются лишь для облегчения восприятия больших чисел.

Поштучно считать предметы удобно тогда, когда их не очень много. Пересчитывать же таким образом большие совокупности скучно и утомительно, поэтому возникла идея объединять единицы в группы. Появился счёт пятёрками, десятками, двадцатками - по количеству пальцев рук и ног "счетовода".

Иероглифическая система Древних Египтян

Около 3 - 2,5 тыс. лет до новой эры древние египтяне придумали свою числовую систему. В ней ключевые числа: 1, 10, 100 и т.д. - изображались специальными значками - иероглифами. Египтяне высекали их на стенах погребальных камер, писали тростниковым пером на свитках папируса.

Для записи чисел египтяне употребляли следующие иероглифы:

Все остальные числа составлялись из этих ключевых при помощи операции сложения.

Величина числа, записанного в иероглифической системе, не зависит от того, в каком порядке расположены составляющие его знаки. Даже если записать их справа налево, один под другим или вперемешку - число от этого не изменится.

Среди множества иероглифических систем счисления, которые существовали в разные времена у разных народов, только одна используется до сих пор. Её цифры знакомы всем, хотя им уже около 2,5 тысячелетий. Эти цифры встречаются на циферблатах часов, фронтонах старинных и современных зданий, памятниках, страницах книг. Речь идет о римской системе счисления.

Римские цифры

Как читать римские цифры? Одно из правил записи римских чисел гласит: "Если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае меньшая цифра не может повторяться), то меньшая вычитается из большей". К примеру, VII = 5 +1 + 1 = 7; IX = 10 - 1 = 9.
Тут мы сталкиваемся с любопытным феноменом: разрешив цифрам при "сборке" чисел не только складываться, но и вычитаться, мы лишились одного из важных математических свойств - единственности представления. Число 1995 мы можем записать как MCMXCV, а так же как MVM, или как MDVD.
Если проанализировать множество старинных и современных надписей римскими цифрами, то можно убедиться, что авторы, старательно скомпоновавшие эти цифры в числа, придерживались каких-то негласных правил. Но единых и чётких правил записи римских чисел нет.

У иероглифической системы представления чисел есть один весьма существенный недостаток: арифметические действия над такими числами - занятие весьма трудоёмкое. Этого неудобства нет у позиционных систем.

Шестидесятеричная Вавилонская система

Идея приписывать цифрам разные величины в зависимости от того, какую позицию они занимают в записи числа, впервые появилась в III тысячелетии до н. э. в Месопотамии (Междуречье) у древнего талантливого народа - шумеров. От них она перешла к вавилонянам - новым хозяевам Междуречья, почему и вошла в историю как вавилонская система счисления.

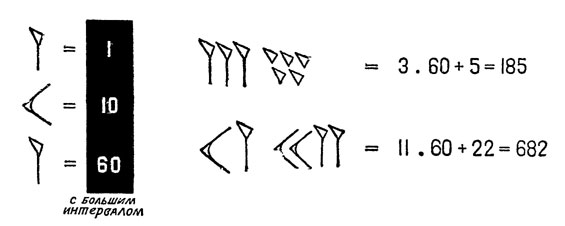
До нас дошли сотни тысяч обожённых глиняных табличек с письменами древних вавилонян. Простейшими цифрами в их системе служили два знака: вертикальный клин - для обозначения 1 и горизонтальный клин - для 10. Числа от 1 до 59 записывались с помощью этих двух знаков, как в обычной иероглифической системе. Число 60 снова обозначалось тем же значком, что и 1. Так же записывались и все другие степени 60: 3600 = 60^2, 216000 = 60^3 и т.д.

Однако из-за отсутствия нуля эта система записи была неоднозначной. В зависимости от контекста одна и та же запись могла означать число 72, или 4320 = 1*60^2 + 12*60^1.

Шестидесятеричная система применялась в астрономических расчетах вплоть до эпохи Возрождения. Ею пользовался во II в. греческий математик Клавдий Птолемей при составлении таблицы синусов, древнейшей из дошедших до нас.

Позиционная десятичная система

Древнейшая известная запись в позиционной десятичной системе обнаружена в Индии и датируется 595 г. Появление хорошо знакомого нам нуля было подготовлено системами счисления, издавна применявшимися не только в Индии, но и в Древнем Китае. В этих старинных системах для записи одинакового числа единиц, десятков, сотен или тысяч использовались одни и те же символы, но дополнительно помечалось в каком разряде они стоят. Постепенно заметили, что даже если не указывать имена разрядов, то число всё равно можно прочитать, так как у каждого разряда есть своя позиция. А если позиция пустая, то её нужно пометить специальным значком - нулём. В поздних вавилонских текстах стал появляться такой знак, однако в конце числа его никогда не ставили. Лишь в Индии в IX
Индийская нумерация пришла сначала в арабские страны, а затем и в Западную Европу. О ней подробно рассказал среднеазиатский математик аль-Хорезми. Простые и удобные правила сложения и вычитания сколь угодно больших чисел, записанных в позиционной системе, сделали её особенно популярной. А поскольку труд аль-Хорезми был написан на общем для мусульманского мира языке - арабском, то за индийской нумерацией в Европе закрепилось неправильное название - "арабская".